INTRODUCTION

Finite element (FE) models of intervertebral discs (IVD) are inherently complex, requiring multiple tissue parameters to be defined for tissues which can be difficult to characterise experimentally. Due to this complexity, understanding how each parameter combines to produce the overall mechanics of the IVD is challenging.  To overcome these challenges we used the super-element approach to provide a novel means of interrogating the IVD mechanics. Of particular interest in the current study, was the coupled, three dimensional (3D) mechanical response of the lumbar spine IVD and to what extent the 3D IVD stiffness is reliant upon the collagen fibre network.

METHODS

A physiologically realistic FE model of the L1-L2 IVD was developed.  Geometry of the IVD represented the NIH Visible Human Project, Visible Man. Figure 1 shows the geometry and mesh of the IVD. The nucleus pulposus was modelled using 3D hydrostatic fluid elements, the annulus fibrosis ground matrix with 3D solid continuum elements, and the collagen fibres with tension only rebar elements.  The rebar elements were embedded at ±30° to the transverse plane of endplates, to represent the alternatively angled collagen fibre network. Collagen fibre spacing and cross-sectional area was based on [2].  The annulus fibrosis was treated as a Mooney-Rivlin hyperelastic material ( MPa,  MPa) and the collagen fibres as linear-elastic (tension only,  MPa).  Further details of the FE modelling can be found in [1].  Nodes representative of the superior and inferior end plates where constrained to a single node located at the centre of the respective end plate (referred to as control nodes).

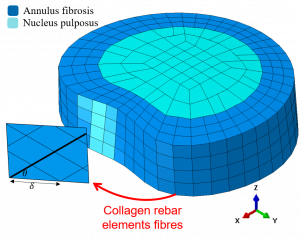
Figure 1:  FE model of the IVD showing the annulus (with collagen fibre angle) and nucleus mesh.

In the super-element approach, degrees of freedom (DOF) of the FE model’s stiffness matrix are decomposed, retaining only the desired DOF. Here, a super element was constructed, retaining only the DOF of the control nodes. In this sense, the FE stiffness matrix can be simplified to a stiffness matrix in terms of just the loads and displacements acting on the superior and inferior surfaces of the IVD.

To explore the power of this approach, a parametric study was conducted to determine the influence of model parameters on the IVD behaviour.  This provides a very effective way of elucidating the contribution of each individual component. Three parameters were investigated; collagen fibre stiffness (250 to 500 MPa), collagen fibre angles (15° to 60°), and ground matrix stiffness  (0.35 to 0.7 MPa).

RESULTS AND DISCUSSION

Through the results of the parametric study, it was demonstrated how the super-element, stiffness-matrix approach is a powerful tool for interrogating the IVD mechanics.  The study further demonstrates how the stiffness matrix can be visualised, providing a powerful technique for understanding the complex coupled motions of the IVD.  The parametric study were able to identify several key model features: (i) collagen fibre stiffness plays a significant role in transverse stiffness, but play a lesser role in axial stiffness; (ii) a clear coupling between axial and transverse motion was observed, which was not significantly affected by fibre stiffness; and (iii) collagen fibre angle has a significant effect on IVD stiffness in all directions and on motion coupling.

CONCLUSIONS

The super-element stiffness matrix approach allows direct extraction of the underlying stiffness matrix which is advantageous in exploring the complex 3D behaviour of the IVD.  This method of stiffness matrix extraction has several direct applications including as inputs for musculoskeletal modelling, benchmarking for artificial IVDs, and providing a powerful tool for exploring the complex 3D behaviour of the IVD.  This approach can be effectively extended to analyse other tissue behaviour, such as the functional spinal unit.

REFERENCE

1. J Little, Computer Methods in Biomechanics and Biomedical Engineering, 11, 95-103, 2008
2. Marchand, F, Ahmed, A., Spine, 15(5), 412, 1990.